Methods
Note: Find the full citations for papers listed below in References. Find tables referenced below in the main file listing page.
USDA's Economic Research Service (ERS) has constructed accounts for the farm sector consistent with a gross output model of production (see Shumway et al. 2017, Ball et al. 2016). Output is defined as gross production leaving the farm, as opposed to real value added. Inputs are not limited to labor and capital but include intermediate inputs as well. Intermediate goods produced and consumed within the farm are self-cancelling transactions and, therefore, do not enter either output or input accounts.
ERS defined the farm sector in the same way as in the National Income and Product Accounts (NIPA). This means that minor goods and services (i.e., secondary outputs) for agriculture that are primary to other industries were included in the primary industry’s output.
There are a few exceptions in the national productivity statistics, however, that we take the existence of certain (inseparable) secondary activities into account when measuring the productive activity of the sector. These activities are defined as activities whose costs cannot be separately observed from those of the primary agricultural activity (see United Nations Revised System of National Accounts, 2008). Examples include machine services for hire, custom feeding of livestock, farm forestry, and recreational activities involving the means of production. The output of the sector thus results from two kinds of activities: agricultural activities, whether primary or secondary, and non-agricultural (or secondary) activities of farms.
Regarding State-level productivity estimates, Ball et al. (2004) estimated each State's growth and relative level of productivity for the period 1960-1999 using an index number approach. ERS applied the methods proposed by Caves, Christensen, and Diewert (1982) and Ball et al. (2004) to extend the State productivity statistics through 2004 (the last year for which State-level statistics were produced).
The next section is organized by component measures. Except where indicated, the methods described apply equally to States and the U.S. farm sector:
- Output
- Intermediate Input
- Labor Input
- Capital Input
- Land Input
- Strengths and Limitations
- Suggested Citation
Output
The output measure begins with disaggregated data for physical quantities and market prices of agricultural goods. The output quantity for each crop and livestock category consists of quantities of commodities sold off the farm (including unredeemed Commodity Credit Corporation loans), additions to inventory, and quantities consumed as part of final demand in farm households during the calendar year. Off-farm sales in the aggregate accounts are defined only in terms of output leaving the sector, while off-farm sales in the State accounts also include sales to the farm sector in other States.
The corresponding price reflects the value of that output to the producer, as subsidies are added and indirect taxes are subtracted from market values. The measure of output also includes goods and services of non-agricultural (or secondary) activities when these activities cannot be distinguished from the primary agricultural activity. Törnqvist indices of output are formed by aggregating over agricultural goods output and the output of goods and services of inseparable secondary activities using revenue-share weights on shadow prices—the prices farmers actually receive or face for each commodity that reflects the market value, the Government subsidy, and/or Government tax (or tax rebate) for that commodity as indicated above.
Intermediate Input
Intermediate input consists of goods used in production during the calendar year, whether withdrawn from beginning inventories or purchased from outside the farm sector or, in the case of the State production accounts, from farms in other States. Open-market purchases of feed and seed inputs enter both State and aggregate farm sector intermediate inputs accounts. Withdrawals from producers' inventories are also measured in output, intermediate input, and capital input. Beginning inventories of crops and livestock represent capital inputs and are treated in the discussion of capital below. Additions to these inventories represent deliveries to final demand and are treated as part of output. Goods withdrawn from inventory are symmetrically defined as intermediate inputs and recorded in the farm input accounts.
Data on current dollar consumption of petroleum fuels, natural gas, and electricity in agriculture are compiled for each State for the period 1960-2004, and for 1948–2021 at the national level. Prices of individual fuels are taken from the Energy Information Administration's Monthly Energy Review. The index of energy consumption is formed implicitly as the ratio of total expenditures (less State and Federal excise tax refunds) to the corresponding price index.
Pesticides and fertilizers have undergone significant changes in quality over the study period. For example, newer types of pesticides may require less mammalian toxicity that poses a less health threat to farm workers and wildlife (Fernandez-Cornejo et al., 2014). In order to measure input price and quantity in constant-efficiency units, we construct price indices for fertilizers and pesticides using hedonic methods. Under this approach, a good or service is viewed as a bundle of characteristics which contribute to the productivity (utility) derived from its use. Its price represents the valuation of the characteristics "that are bundled in it," and each characteristic is valued by its "implicit" price (Rosen, 1974). However, these prices are not observed directly and must be estimated from the hedonic price function.
A hedonic price function expresses the price of a good or service as a function of the quantities of the characteristics it embodies. Thus, the hedonic price function for, say pesticides, may be expressed as Wp = W(X, D), where Wp represents the price of pesticides, X is a vector of characteristics or quality variables, and D is a vector of other variables that may affect price.
Kellogg et al. (2002) have compiled data on characteristics that capture differences in pesticide quality. These characteristics include toxicity, persistence in the environment, and leaching potential, among others.
Other variables (denoted by D) are also included in the hedonic equation, and their selection depends not only on the underlying theory but also on the objectives of the study. If the main objective of the study is to obtain price indices adjusted for quality, as in our case, the only variables that should be included in D are time or State dummy variables, which will capture all price effects other than quality. After allowing for differences in the levels of the characteristics, the part of the price difference not accounted for by the included characteristics will be reflected in the coefficients on the dummy variables.
Economic theory places few if any restrictions on the functional form of the hedonic price function. We adopt a generalized linear form, where the dependent variable and each of the continuous independent variables is represented by the Box-Cox transformation. This is a mathematical expression that assumes a different functional form depending on the transformation parameter, and which can assume both linear and logarithmic forms, as well as intermediate non-linear functional forms.
Thus the general functional form of our model is given by:
where is the Box-Cox transformation of the dependent price variable, Wp > 0; that is,
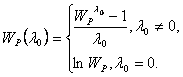
Similarly, 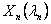 is the Box-Cox transformation of the continuous quality variable
is the Box-Cox transformation of the continuous quality variable 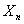 where
where 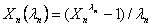 if
if 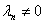 and
and 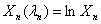 if
if 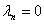 . Variables represented by D are time dummy variables, not subject to transformation;
. Variables represented by D are time dummy variables, not subject to transformation; 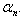 and
and 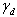 are unknown parameter vectors, and
are unknown parameter vectors, and 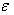 is a stochastic disturbance.
is a stochastic disturbance.
Finally, price and implicit quantity indices are constructed for purchased services, such as purchased contract labor services, purchased machine services, and maintenance and repairs. Available data are limited to nominal expenditures for various services. To decompose expenditures for contract labor services into price and quantity components, we estimate a hedonic wage function where hourly earnings are expressed as a function of demographic characteristics including sex, age, education, experience, as well as legal status using National Agricultural Worker Survey data (see Wang et al. 2013b for further discussion). Purchased machine services substitute for own capital input. Therefore, we construct the implicit quantity of purchased machine services as the ratio of expenditures to an index of rental prices of agricultural machinery (i.e., farm tractors or agricultural machinery excluding tractors). Translog indices of intermediate input are constructed by weighting the growth rates of each category of intermediate input described above by their value share in the overall value of intermediate inputs.
Labor Input
The USDA labor accounts for the aggregate farm sector incorporate the demographic cross-classification information of the agricultural labor force. Matrices of hours worked and compensation per hour have been developed for laborers cross-classified by sex, age, education, and employment class—employee versus self-employed and unpaid family workers. This was accomplished by incorporating data from both establishment and household surveys using the RAS procedure (see Jorgenson, Gollop, and Fraumeni (1987:72-76) for more discussion) and cross-entropy method. The farm sector matrices with demographic information were taken from the Census of Population (U.S. Department of Commerce, U.S. Census Bureau) and the American Community Survey (ACS) in more recent years. The resulting estimates of employment, hours worked, and labor compensation are controlled to the total numbers for the farm sector based on establishment surveys that underlie the U.S. National Income and Product Accounts (NIPA) and special tabulation work by Bureau of Labor Statistics (BLS) derived from the Current Population Survey (CPS).
In addition, ERS has developed a set of similarly formatted but otherwise demographically distinct matrices of labor input and labor compensation by State. This is accomplished using the RAS procedure (Jorgenson, Gollop, and Fraumeni (1987)) by combining the aggregate farm sector matrices with State-specific demographic information available from the decennial Census of Population (U.S. Department of Commerce). The result is a complete State-by-year panel data set of annual hours worked and hourly compensation matrices with cells cross-classified by sex, age, education, and employment class and with each matrix controlled to the USDA hours-worked and compensation totals, respectively.
Indices of labor input were constructed for each State and the aggregate farm sector using the demographically cross-classified hours and compensation data. Labor hours having higher marginal productivity (wages) are given higher weights in forming the index of labor input than are hours having lower marginal productivities. Doing so explicitly adjusts indices of labor input for "quality" change in labor hours as originally defined by Jorgenson and Griliches (1967).
Capital Input
This study requires measures of capital input and capital service prices for each State and the aggregate farm sector. Construction of these series begins with estimating the capital stock and rental price for each asset type. For depreciable assets, the perpetual inventory method (United Nations, 2009) is used to develop stocks from data on investment For land and inventories, capital stocks are measured as implicit quantities derived from balance sheet data. Implicit rental prices for each asset are based on the correspondence between the purchase price of the asset and the discounted value of future service flows derived from that asset.
Depreciable Assets
Under the perpetual inventory method, capital stock at the end of each period, Kt , is measured as the sum of all past investments, each weighted by its relative efficiency, :
where is approximated by a hyperbolic efficiency function
and where L is the service life of the asset, τ represents the asset's age, and β is a curvature or decay parameter. The value of β is restricted only to values less than or equal to one. For values of β greater than zero, the efficiency of the asset approaches zero at an increasing rate. For values less than zero, efficiency approaches zero at a decreasing rate.
Little empirical evidence is available to suggest a precise value for β. However, two studies (Penson, Hughes and Nelson, 1977; Romain, Penson and Lambert, 1987) provide evidence that efficiency decay occurs more rapidly in the later years of service, corresponding to a value of β in the 0 to 1 interval. For purposes of this study, it is assumed that the efficiency of a structure declines slowly over most of its service life until a point is reached where the cost of repairs exceeds the increased service flows derived from the repairs, at which point the structure is allowed to depreciate rapidly (β=0.75). The decay parameter for durable equipment (β=0.5) assumes that the decline in efficiency is more uniformly distributed over the asset's service life.
Consider now the efficiency function that holds β constant and allows L to vary. This concept of variable service lives is related to the concept of investment, where investment is a bundle of different types of capital goods. Each of the different types of capital goods is a homogeneous group of assets in which the actual service life, L, is a random variable reflecting quality differences, maintenance schedules, etc. For each asset type, there exists some mean service life, 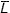 , around which there exists some distribution of actual service lives. In order to determine the amount of capital available for production, the actual service lives and their frequency of occurrence must be determined. It is assumed that the underlying distribution is the normal distribution truncated at points two standard deviations above and below the mean service life.
, around which there exists some distribution of actual service lives. In order to determine the amount of capital available for production, the actual service lives and their frequency of occurrence must be determined. It is assumed that the underlying distribution is the normal distribution truncated at points two standard deviations above and below the mean service life.
The other critical variable in the efficiency function is asset lifetime L. For each asset type, there exists some mean service life, 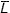 , around which there exists some distribution of actual service lives. It is assumed that the underlying distribution is the normal distribution truncated at points two standard deviations above and below the mean service life. Mean service lives correspond to 85 percent of the U.S. Department of the Treasury’s "Bulletin F" lives.
, around which there exists some distribution of actual service lives. It is assumed that the underlying distribution is the normal distribution truncated at points two standard deviations above and below the mean service life. Mean service lives correspond to 85 percent of the U.S. Department of the Treasury’s "Bulletin F" lives.
Capital Rental Prices
Firms will add to their capital stock so long as the present value of the net revenue generated by an additional unit of capital exceeds the purchase price of the asset. This can be stated algebraically as:
where p is the price of output (y), 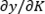 is the marginal product of capital K so the gross revenue in each period will rise by
is the marginal product of capital K so the gross revenue in each period will rise by 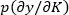 with an additional unit of K; wK is the price of investment assets,
with an additional unit of K; wK is the price of investment assets, 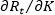 is the increase in replacement (R) in period t required to maintain the capital stock at the new level, so net revenue will rise by only
is the increase in replacement (R) in period t required to maintain the capital stock at the new level, so net revenue will rise by only 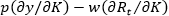 ; and r is the real discount rate. To maximize net present value, firms will continue to add to capital stock until this equation holds as an equality (Ball et al., 2016):
; and r is the real discount rate. To maximize net present value, firms will continue to add to capital stock until this equation holds as an equality (Ball et al., 2016):
where c is defined as the implicit rental price of capital.
The rental price consists of two components. The first term, rwK, represents the opportunity cost associated with the initial investment.
The second term, is the present value of the cost of all future replacements required to maintain the productive capacity of the capital stock.
Let F denote the present value of the stream of capacity depreciation on one unit of capital according to the mortality distribution m:
where 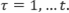
Since replacement at time t is equal to capacity depreciation at time t:
so that
The real rate of return, r in the above expression, is calculated as the nominal yield on investment grade corporate bonds less the rate of inflation as measured by the asset specific prices. An ex ante rate is then obtained by expressing observed real rates as an ARIMA process. We calculate F holding the required real rate of return constant for that vintage of capital goods. In this way, implicit rental prices c are calculated for each asset type (except for inventory, where the rate of inflation is measured by the implicit deflator for gross domestic product for data consistency). Asset prices and investment data are drawn from BLS, ERS, and NASS.
Finally, indices of capital input for each State and the aggregate farm sector are constructed by aggregating over the different capital assets using the asset-specific rental prices as weights.
Land Input
To obtain a constant-quality stock of land, we compile data on land area and average value (excluding buildings) per acre for each county in each State. The land area in each county is reported in the Census of Agriculture. Data for years intermediate to the censuses are obtained using cubic spline interpolation. However, the Census only reports data on the value of farm real estate (i.e., land and structures); it does not provide data on land values separately. Historically, the value of farm real estate was partitioned into its components using information from the Agricultural Economics and Land Ownership Survey (AELOS). However, AELOS was last conducted in 1999. We now rely on the annual USDA, Agricultural Resource Management Survey to derive estimates of the value of land from data on the value of farm real estate.
Differences in the quality of land across States and regions prevent the direct comparison of observed prices. To account for these quality differences, we calculate relative prices of land from hedonic regression results.
As noted above, the hedonic approach views land as a bundle of characteristics which contribute to output derived from its use. The World Soil Resources Office of the USDA's Natural Resources Conservation Service (NRCS) has compiled data on land characteristics (see Eswaren, Beinroth, and Reich (2003)). They develop a procedure for evaluating inherent land quality, and use this procedure to assess land resources on a global scale. Given the Eswaren, Beinroth, and Reich database, we use GIS to overlay State and county boundaries. The result of the overlay gives us the proportion of land area of each county that is in each of the soil stress categories. These characteristics include soil acidity, salinity, and moisture stress, among others. The "level" of each characteristic is measured as the percentage of the land area in a given region that is subject to stress. A detailed description of the characteristics included in the hedonic model is provided in Ball et al. (2008). The environmental attributes most highly correlated with land prices in major agricultural areas are moisture stress and soil acidity. In areas with moisture stress, agriculture is not possible without irrigation. Hence irrigation (i.e., the percentage of the cropland that is irrigated) is included as a separate variable. Because irrigation mitigates the negative impact of acidity on plant growth, the interaction between irrigation and soil acidity is included in the vector of characteristics (Ball et al., 2008).
In addition to environmental attributes, we also include a "population accessibility" score for each county in each State. These indices are constructed using a gravity model of urban development, which provides a measure of accessibility to population concentrations. A gravity index accounts for both population density and distance from that population. The index increases as population increases and/or distance from that population center decreases.
Strengths and Limitations
This dataset provides the official USDA statistics on agricultural outputs, inputs, and total factor productivity for the U.S. farm sector. This is the only source of a long-term agricultural TFP series spanning the 1948-2021 period for the aggregate sector. Input measures are adjusted for changes in their quality, such as improvements in the efficacy of chemicals, or changes in the demographics of the farm workforce. The formatted tables provide a quick reference for comparing the latest data to historical figures, and the comma separated values (CSV) files provide a full and detailed dataset that can be used by programmers for thorough data analysis.
Because of data limitations, this dataset does not account for output quality changes. In the short-term, measured agricultural productivity can also be affected by random events like adverse weather events or business cycles, among other factors that are not captured in the data series.
Recommended Citation
U.S. Department of Agriculture, Economic Research Service. Agricultural Productivity in the U.S., January 12, 2024.

